- Tujuan praktikum
Menentukan nilai gravitasi bumi menggunakan aplikasi phyphox
- Dasar teori
Gerak bandul merupakan gerak harmonik sederhana atau system mekanik melalui suatu titik kesetimbangan. Sistem mekanik dapat bergerak secara periodik yang diakibatkan oleh bekerjanya gaya pemulih pada sistem tersebut. Gaya pemulih yang bekerja adalah sebanding terhadap kedudukan relatif massa sistem terhadap titik kesetimbangan dan selalu berarah menuju titik kesetimbangan tersebut. Gerak ini disebut sebagai gerak osilasi harmonis sederhana. Secara umum sistem mekanik dapat digambarkan oleh sistem bandul matematis dan sistem pegas-massa seperti yang ditunjukan Gambar.1. memperlihatkan bandul sederhana yang terdiri dari tali dengan panjang l dan beban bermassa m. Gaya yang bekerja pada beban adalah beratnya m.g dan tegangan T pada tali. Bila tali membuat sudut θ terhadap vertikal,berat memiliki komponen komponen mgcos θ sepanjang tali dan mgsin θ tegak lurus tali dalam arah berkurangnya θ.
Pendulum berosilasi akibat adanya komponen gaya berat m.g sin θ. Karena tidak ada gaya gesekan udara, maka pendulum melakukan osilasi dengan besar amplitudo tetap sama.
Gaya yang bekerja pada partikel itu adalah beratnya (mg) dan tegangan tali T .Berdasarkan gambar.1, maka pada komponen tangensial dari mg terdapat gaya :
Tanda (-) menyatakan bahwa arah F selalu berlawanan dengan perpindahan.Berdasarkan Hukum II Newton tentang gerak, persamaan gerak pada arahtangensial memenuhi persamaan :
Dengana tadalah percepatan partikel pada arah tangensial. Selama partikelberpindah sepanjang lingkaran berjari-jaril, maka berlaku :
Subsitusikan pers (1.2) dan (1.3) dengan menyamakan pers (1.1) maka persamaan gerak partikel menjadi
Atau
Agar bandul berayun secara kontinu, maka sudut simpangan θ harus sangat kecilrelatif terhadap panjang talil.untuk θ makasin θ≈θ, sehingga persamaan ( 1. 5 ) menjadi
Persamaan diferensialyangmewakili gerakan osilasi bandul harmonik sederhanadengan frekuensi osilasi memenuhi persamaan:
Ket
ω = frekuensi sudut osilasi (Hz)
T = periode osilasi (s)
g = percepatam gravitasi (m/s^2) (9,8 m/s^2)
l = panjang tali bandul (m)
Jika persamaan ( 1.7 ) dinyatakan dalam bentuk periode T osilasi bandul harmonis sederhana dengan T=2π⁄ω maka diperoleh
Secara umum gerak osilasi sederhana system bandul mathematis dinyatakan dengan rumus sebagai berikut :
Dengan suatu pendekatan bahwa sudut simpangan bandul relatif kecil terhadappanjang tali, maka berdasarkan persamaan (2.11) dapat dilakukan perhitunganbesarnya percepatan gravitasi bumi(g)melalui pengukuran periode ayunan (T)berdasarkan variasi (l).
- Alat dan bahan
- Smartphone
- Aplikasi Phyphox
- Tali rafia (2 meterr)
- Penggantung untuk menggantung beban
- Penggaris
- Busur
- Prosedur eksperimen
- Instal Apk Phyphox
- Membuka Apk Phypox, lalu muncul tampilan awal pada apk PhyphoxGambar 2. Layar utama Apk Phyphox
- Lalu pilih Pendulum dengan mengklik pada tulisan Pendulum gambar 3. menu pendulum
5. kemudian klik pada titik tiga kemudian klik pada Timed run, atur waktu start dan lama durasi sesuai keinginan
6. Setelah itu akan kembali ketampilan awal, kemudian persiapkan alat praktikum dengan cara memberikan tali pada hp, kemudian klik tombol start lalu pada waktu ke 1s benda digerakkan ke kanan dan kekiri
7. setelah benda berhenti maka data yang akan muncul kemudian catat data yang telah diperoleh, setelah itu lakukan percobaan tersebut sampai 5 kali dengan periode yang berbeda-beda
- Data percobaan
1. Percobaan dengan Panjang tali 40 sudut 300 dengan t= 20s
|
Percobaan |
Panjang Tali |
Gravitasi |
|
1 |
40 |
|
|
2 |
40 |
|
|
3 |
40 |
|
|
4 |
40 |
|
|
5 |
40 |
|
|
RATA-RATA |
|
|
2. Percobaan dengan Panjang tali 50 sudut 300 dengan t= 20s
|
Percobaan |
Panjang Tali |
Gravitasi |
|
1 |
50 |
|
|
2 |
50 |
|
|
3 |
50 |
|
|
4 |
50 |
|
|
5 |
50 |
|
|
RATA-RATA |
|
|
3. Percobaan dengan Panjang tali 60 sudut 300 dengan t= 20s
|
Percobaan |
Panjang Tali |
Gravitasi |
|
1 |
60 |
|
|
2 |
60 |
|
|
3 |
60 |
|
|
4 |
60 |
|
|
5 |
60 |
|
|
RATA-RATA |
|
|
- Pembahasan
……………………………………………………………………………………………………………………………………………………………………………………………………
- Kesimpulan dan Saran
…………………………………………………………………………………………………
…………………………………………………………………………………………………









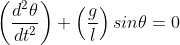








0 komentar:
Posting Komentar